The full World Championship match results:

Get rythm (Joaquin Phoenix / Johnny Cash)
Hey get rhythm when you get the blues
C'mon get rhythm when you get the blues
Get a rock and roll feelin' in your bones
Get taps on your toes and get gone
Get rhythm when you get the blues
A little shoeshine boy he never gets lowdown
But he's got the dirtiest job in town
Bendin' low at the people's feet
On a windy corner of a dirty street
Well I asked him while he shined my shoes
How'd he keep from gettin' the blues
He grinned as he raised his little head
He popped his shoeshine rag and then he said
Get rhythm when you get the blues
C'mon get rhythm when you get the blues
Yes a jumpy rhythm makes you feel so fine
It'll shake all your troubles from your worried mind
Get rhythm when you get the blues
Get rhythm when you get the blues
Get rhythm when you get the blues
C'mon get rhythm when you get the blues
Get a rock and roll feelin' in your bones
Get taps on your toes and get gone
Get rhythm when you get the blues
Well I sat and listened to the sunshine boy
I thought I was gonna jump with joy
He slapped on the shoe polish left and right
He took his shoeshine rag and he held it tight
He stopped once to wipe the sweat away
I said you mighty little boy to be a workin' that way
He said I like it with a big wide grin
Kept on a poppin' and he'd say it again
Get rhythm when you get the blues
C'mon get rhythm when you get the blues
It only cost a dime just a nickel a shoe
It does a million dollars worth of good for you
Get rhythm when you get the blues
For the good times (Kris Kristofferson)
Don't look so sad. I know it's over
But life goes on and this world keeps on turning
Let's just be glad we had this time to spend together
There is no need to watch the bridges that we're burning
Lay your head upon my pillow
Hold your warm and tender body close to mine
Hear the whisper of the raindrops
Blow softly against my window
Make believe you love me one more time
For the good times
I'll get along; you'll find another,
And I'll be here if you should find you ever need me.
Don't say a word about tomorrow or forever,
There'll be time enough for sadness when you leave me.
Lay your head upon my pillow
Hold your warm and tender body Close to mine
Hear the whisper of the raindrops
Blow softly against my window
Make believe you love me
One more time
For the good times
STABELVOLLEN MEDIA
Copyright of all music videoes, guest photoes and artworks solely belongs to the artists. Copyright of all other resources : Stabelvollen Media.
EDUCATIONAL RESOURCES IN MATHEMATICS - ALGEBRA
There's a beautiful link between the mathematical subjects Geometry and Algebra. Historically this link was originally shown first by the french Philosopher and Mathematician Rene Descartes. (1596 - 1650)
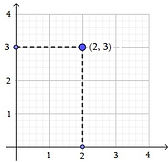
Descartes showed how geometric points can be represented in a coordinate system as two linked coordinates, the first one showing the point relative to a vertical axis of the coordinate system, and the second coordinate showing the point relative to the horisontal axis.
Thus the point with coordinates 2 and 3, that is the point (2, 3) is situated 2 unites to the right of the
vertical axis and 3 units above the horisontal axis.
Representing geometrical points in this way, also makes it possible to represent functional relations in abeautiful and effective way.
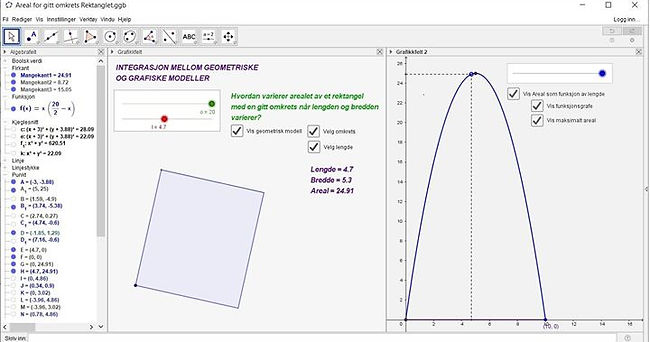
The picture above shows how the area of a square as a function of it's edge-length can be representated dynamically in the multirepresentational dynamic environement GeoGebra. The edge-length can be changed dynamically producing a second degree function graph (to the right) showing dynamically how the square area changes as the edge-length is changed.
The app which can be used within GeoGebra or as an online app, can be bought from Stabelvollen
Media and be used freely, privately only. Purcahse the app in SHOP, and the app can be downloaded online.
(c) : Stabelvollen Media. 2020.