
The full World Championship match results:

Get rythm (Joaquin Phoenix / Johnny Cash)
Hey get rhythm when you get the blues
C'mon get rhythm when you get the blues
Get a rock and roll feelin' in your bones
Get taps on your toes and get gone
Get rhythm when you get the blues
A little shoeshine boy he never gets lowdown
But he's got the dirtiest job in town
Bendin' low at the people's feet
On a windy corner of a dirty street
Well I asked him while he shined my shoes
How'd he keep from gettin' the blues
He grinned as he raised his little head
He popped his shoeshine rag and then he said
Get rhythm when you get the blues
C'mon get rhythm when you get the blues
Yes a jumpy rhythm makes you feel so fine
It'll shake all your troubles from your worried mind
Get rhythm when you get the blues
Get rhythm when you get the blues
Get rhythm when you get the blues
C'mon get rhythm when you get the blues
Get a rock and roll feelin' in your bones
Get taps on your toes and get gone
Get rhythm when you get the blues
Well I sat and listened to the sunshine boy
I thought I was gonna jump with joy
He slapped on the shoe polish left and right
He took his shoeshine rag and he held it tight
He stopped once to wipe the sweat away
I said you mighty little boy to be a workin' that way
He said I like it with a big wide grin
Kept on a poppin' and he'd say it again
Get rhythm when you get the blues
C'mon get rhythm when you get the blues
It only cost a dime just a nickel a shoe
It does a million dollars worth of good for you
Get rhythm when you get the blues
For the good times (Kris Kristofferson)
Don't look so sad. I know it's over
But life goes on and this world keeps on turning
Let's just be glad we had this time to spend together
There is no need to watch the bridges that we're burning
Lay your head upon my pillow
Hold your warm and tender body close to mine
Hear the whisper of the raindrops
Blow softly against my window
Make believe you love me one more time
For the good times
I'll get along; you'll find another,
And I'll be here if you should find you ever need me.
Don't say a word about tomorrow or forever,
There'll be time enough for sadness when you leave me.
Lay your head upon my pillow
Hold your warm and tender body Close to mine
Hear the whisper of the raindrops
Blow softly against my window
Make believe you love me
One more time
For the good times
STABELVOLLEN MEDIA
Copyright of all music videoes, guest photoes and artworks solely belongs to the artists. Copyright of all other resources : Stabelvollen Media.
MODELING THE EARTH

MODELLING THE SHAPE OF THE EARTH
"The Earth is round- like a pizza!" (Mickey Mous in Goofy Columbus.)
Most people is of courde familiar with the fact that we live on a globe that is roughly sperical, and nevertheless, the immediate experience is that (if we disregard mountains and valleys) the landscape in a limited but relatively large area around us is largely flat.
Throughout history, this has also given rise to beliefs that the earth is in reality flat (like a pancake).
Everyone has heard the story of when Christopher Columbus wanted to sail west to find the sea route to India - a country to the east. Columbus' bright idea was that you could sail around the world to the west and thus not have to sail around the Horn of Africa.
But in people's eyes, there was one big snag in the plan: The earth was flat, that's what most people thought in Columbus' time. Therefore they also believed that he could not travel west to India, but would sail over the edge of the world and disappear into the abyss.
Eks. A simple experiment can convince us that the notion of a flat
earth does not hold true. (see fig. below) Glue two sticks /
matches some distance apart on a piece of paper and light
vertically down towards the paper (parallel to the pins). You
cannot observe any shadow as long as there is light parallel
to the pins. Then bend the paper as shown right and light
again perpendicular to the paper, You can then observe
shade from at least one of the pins.

EARTH CURVATURE I

Eratosthenes was able to find out that the earth must have the shape of a sphere. This is easily observable if we see a ship approaching on the horizon. The top of the mast then becomes visible first and then gradually the rest of the ship. We can also calculate how far a lookout in the masthead can see (or put another way how far away the ship is when the masthead just comes into view.)
The length of the line of sight from the masthead, B, to the lookout's horizon, A, is always lateral in a triangle where the third corner is the center of the earth.
The length of the line of sight (AB) can be determined through a simple application of Pythagoras' theorem for right-angled triangles (see fig.)
In triangle SAB we see that:
Also, SA = radius of earth and SB = SC + BC = 6400 + h. This gives us:
(Here, all sizes are calculated in km.)Notice:
Since is very small compared to
we can disregard this term in the calculation, and get:
As an example we can think of a sailing ship with a masthead that is 15 m above sea level, i.e. h = 15 m = 0.015 km.
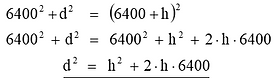
Then
Note that for further accuracy the formula must actually be adjusted somewhat due to the refraction of light in the atmosphere, but we choose to ignore that here.
EARTH CURVATURE II
Examples




Fot the biggest lake in North-Trondelag county in Norway, Snåsavatnet, the longest distance across this lake is 89,7 km long (The curve distance AB in the fig. to the left).
The average earth radius, r = 6378,395 km. In the grey-shaded (right-angled) triangle, we have, using Pythagoras' sentence:
which gives us that
The water surface of Snåsavatnet has a maximum elevation of 35 m on the longest distance of the lake.

Fot the biggest lake in Norway, Mjøsa, the distance from Minnesund to Lillehammer across Mjøsa is 89,7 km long.
The average earth radius, r = 6378,395 km
a = the part of the earth circumference that the length of Mjøsa constitutes.
b = 0,40275 degrees
cos b = cos 0,40275 = 0,99997529
In the grey-shaded triangle :
cos b = x/r so x = r * cosb and h = r - x so
h = r - r * cosb = r(1 - cosb)
h = 6378,395 km * (1 - 0,99997529) = 0,1576 km = 158 m
So the water surface of Mjøsa has a maximum elevation of 158 m on the Minnesund - Lillehammer section.

ERATOSTHENES AND THE CIRCUMFERENCE OF THE EARTH


Eratosthenes (275 - 194 BC) did approx. 250 BC a famous limitation of the Earth's radius, which in many ways shows how far one had come in knowledge of earth measurement and astronomy.
Eratosthenes' survey of the earth is a link between the laws of geometry, geography and astronomy.
The method built on four simple facts:
1. Rays of light from the sun can be considered to
be parallel, since the distance until the sun is
so large compared to the earth's radius.
2. A straight line intersects parallels at the same
angle.
3. The zenith, the observer and the center of the
earth lie on a straight line.
4. At noon, the sun is in the observer's meridian.
Eratostenes knew that Syene (which is called Aswan today) is 800 km (almost straight) south of Alexandria. (See fig. above)
He had read that in Syene there was a deep well in which the sun reflected on a certain day of the year. Then the sun was at its zenith over Syene. On the same day, the sun's rays formed 7.5 degrees of vertical direction in Alexandria.
The radii from Earth's center to Syene and Alexandria respectively formed an angle of 7.5 degrees with each other. The arc length between Alexandria and Syene along the meridian was 840 km.
Now 72 / 360 = 1/50, so the arc length between Alexandria and Syene is 50th of the entire circumference of the Earth.
Eratosthenes was thus able to find the circumference of the earth: 50 * 800 km = 40,000 km.Since Eratosthenes knew the formula for the circumference of a circle, he could also find the Earth's radius, R, as:R = O / 2pi = 40,000 km / (2 * 3.14) = 6,369 km.This is astonishingly close to the correct average value for Earth's radius of 6,371 km. The error in Eratosthenes' calculation was thus only 100% * (6,371 - 6369) / 6371 = 3.1%.
DELAMBRE AND MECHAIN - DEFINING THE METER

The definition of a meter - a revolutionary idea
During the 17th and 18th century many attempts were made to measure the size of the earth , being either the exact length of a meridian from the North Pole to Equator, the aim being to determine a universallly defined length of a meter.
The most famous attempt is probably the determination of the length of the meridian through Paris during the years 1792 - 1799, among others described in the famous book "The measure of all things" by Ken Adler. (Adler, 2004)
The French Science Academy, inspired by the revolusionary ideas of the time after the French Revolution in 1789, wanted to define the meter-length independent of any human property or interests and by measures of the earth itself. After the work of two famouse french geometers who managed to determine the length (with one later discovered minor measuring mistake) of the distance along the meridian from Dunkurque to Barcelona, and thereby wa able to calculate the distance of the whole meridian with acceptable accuracy.
After this enormous effort, the lenngth of 1 meter then was defined as 1 / 10 000 000 of the distance between the North Pole and Equator along this meridian! In the following years the metric system was built for different kind of measures much as we know it today, with the determination og the meter length as a foundation.

The Measure of All Things tells the story of hoe science, revolutionary politics and the dream of a new economy converged to produce both the metric system and the first struggle over globalization.Amid the scientific fervour of the Revolution two French scientists, Delambre and Mechain, were sent out on an expedition to measure the shape of the world and thereby establish the metre.
As one scientist went north along the Frrench meridian and the other south, they could not know the deadly obstacles that lay ahead. Delambre narrowly escaped the guillotine on the outskirts of Paris, while Mechain was trapped behind enemy lines in the war against Spain and imprisoned.
It was to be seven years before they received a hero's welcome in Paris.
STRUVE AND THE GEODETIC ARC


The first attempt - Struves Gedodetic Arc

A not so well known attempt to determine such a distance took place from 1816 to 1855, is the Struve Geodetic Arc:
It made the very first accurate measurement of a meridian arc.
The so-called Struve Geodetic Arc is a chain of survey triangulations stretching from the city Hammerfest in Northern Norway to The Black Sea.
through ten countries and over 2820 kilometres.
The chain was established and used byt the German-born Russian scientist Friedrich Georg Wilhelm von Struve, aiming to establish the exact size and shape of the earth.
At first the chain passed merely through three countries, Norway, Sweeden and the Russian Empire.The arc's first point is located in Tartu Observatory in Estonia, where Struve conducted much of his research.
The purpose of the Struve Geodetic arcThe pupose of Struve's measurements was to find accurate measures for the shape and size of the earth.
he work continued during the periode 1816 - 1865. It consisted in measuring a great number of angles at a great number of points and calculating positions in 13 measurement pints by astronomical observations towards stars.
Struve's meridian arc is the longest continuous series of degree measurements conducted with classical methods. 34 of the original measring-points is today on the World Inheritage list of UNESCO.
This extensive international cooperation was lead by the german atronomer Friedrich Georg Wilhelm Struve.
The series itself consisted of 265 main points which formed a chain of 258 triangles (plus 60 auxiliary points) roughly along a chosen meridian plane through the observatory at the University of Dorpat (today Tartu in Estonia). The distances in the grid were determined by the transfer of ten bases that were measured very accurately (down to one millimeter per kilometer) using base rods in the toise (French) and sajen (Russian) units of length.The degree measuring line stretches from Stara Nekrasivka (near Izmail) on the Black Sea to Fuglenes (near Hammerfest) on the Arctic Ocean, a distance of 2,821.853 kilometers.The meridian arc today passes through ten countries: Norway, Sweden, Finland, Russia, Estonia, Latvia, Lithuania, Belarus, Moldova and Ukraine.
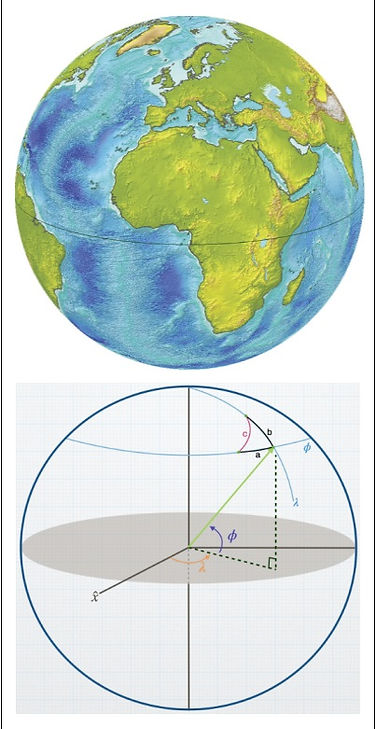
POSISION DETERMINATION ON THE FACE OF THE EARTH
A method to decide the latitude for a random point on the surface of the Northern hemisphere of the is decribed in the figures belwow :

TIME INDICATION BY SHADOW OF THE SUN - SUNDIAL


There are many different types of sundials, both of different shapes and uses. Some are designed for a specific location, some can be moved and need to be set for that particular location, and some are portable.
Most sundials consist of a gnomon that casts a shadow on a dial.It can be a simple bar or an edge on some figure.The dial is usually a flat surface with hour markings.
The hour markers can be adjusted to take the longitude into account.In areas where there is a midnight sun, some types of sundials can be used around the clock in summer.
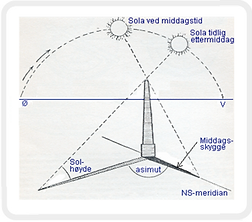
Another important tool for understanding time was the sun's shadow. It always pointed in a certain direction at noon on the day it was shortest.
The midday shadow divided the horizon along a line, the meridian, which runs from due north to due south. (Fig. on the left)
The day with the shortest midday shadow was the summer solstice. (June 21 in our calendar), and a year was counted as the time between two summer solstice.
Besides observing the shadow of the sun during the seasons, man learned to arrange his meals and his work according to the length of the shadow a pole or stone cast over the ground.
At noon on the equinox, (i.e. 21 March and 23 September in our calendar) the sun rises due in the east and sets due in the west. The sun's shadow in the middle of the day always falls on the line connecting the north and south points on the horizon.
This is also the location's meridian. Zenit is what the astronomers call the direction directly above our heads, i.e. perpendicular to the horizontal plane of the place where we are standing.
Note that the angle h, which we call the sun's altitude (the sun's angular height above the horizon) and the angle, S, between the sun's ray and plumb line add up to , i.e. h = 90 degrees - S.
REFERENCES
Alder, K. (2002) The Measure of All Things.The seven year old odyssey that transformed the world. Abacus. London Ken Alder.2002.
Aleksandrov, A.D. (1963) Mathematics. It’s Content, Methods, and Meaning. A.D. Aleklsandrov, A.N. Kolmogorov, M.A. Lavrentev. MIT Press 1963.
Bunt, L.N.H. (1976) The historical roots of elementary mathematics. L.N.H. Bunt, P.S. Jones, J.D. Bedient. Prentice Hall. 1976.
Dolan, G. (2003) On the line. Natinal Maritime Museum. Greenwich, London. Graham Dolan 2003.
Eves, H. (1976) An introduction to the history of mathematics. H. Eves. Holt, Reinhart and Winston. 1976.
Hogben, L. (1937) Matematikk for millioner. Norsk utg. Lancelot Hogben. Gyldendal. 1937.
Johannesen, K. (2016) Jordgeometri. Kompendium. Lærerutdanningen Nord Universitet. Kyrre Johannesen. 2016.
Kehlmann, D. (2008) Oppmålingen av verden. Gyldendal. Oslo. Daniel Kehlmann. 2008
Newman, J.R. (1956) Matematikens kulturhistorie. Sigma / 4. J.R. Newman (ed.) Forum. 1956.
Nygård, J. (1979) Nogle kapitler af matematikens kulturhistorie. Jette Nygård. Århus Universitet. 1979.
Sobel, D. (2005) The true story of a lone Genius Who Solved the Greatest Scientific Problem of His Time. Harper Perennial. Dava Sobel. 2005.


